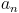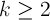Section 9.3 Geometric Sequences

The difference between arithmetic and geometric sequences is that arithemtic sequences has a common difference in each sequence, whereas a geometric sequence has a Common Ratio.

It is a geometric sequence if the ratios of consecutive terms are the same.

 =  .....= r.  r  0


The common ratio here is 2 because as you can see each number multiplied by 2 gives you the next term.

When solving for a certain term or the nth term of a sequence, you would use the equation:

Always remember that r is the common ratio of consecutive terms of a geometric sequence.

A very important equation to remember is The Sum of a Finite Geometric Sequence

The other very important equation to remember from this chapter is the Sum of an Infinite Geometric Series. This equation is very similar to that of the sum of finite geometric sequences. This equation is to be used when r, the common ratio, is less than 0.

This section could not have been learned without the help of the great math teacher: Thad Wilhelm.





9.2

A sequence is arithmetic if the differences between consecutive terms are the same. So the sequence...
a1, a2, a3, a4, a5.... an
is arithmetic if there is a number d such that
a2-a1=a3-a2=a4-a3=...=d
The number d is the commin difference of the arithmetic sequence.


ex: 3, 6, 9, 12
d=3

The nth term of an arithmetic sequence has the form
an=dn+c
where d is the common difference between consecutive terms of the sequence and c is a1-d

the sum of a finite arithmetic sequence with n terms is
sn=(n/2)(a1+an)

this formula only works for arithmetic sequences

ex: 1+3+5+7+9+11+13+15+17+19=sn
=n/2(a1+an)
=10/2(1+19)
=100

Chapter 9: Summation Notation

Letter a is our first index, and letter b is our last index or upper limit. The variable(s) are the letters or the numbers that appear constantly in all terms.

Examples:

1.
2.
3.
4.
5.

Properties of Sums:

c a_n = c a_n c is any constant

a_n + b_n = (a_n + b_n)

a_n - b_n = (a_n - b_n)

Many applications involve the sum of the terms of an infinite sequence. Such a sum is called an infinite series or simply a series.

_{The sum of the first n terms of the sequence is called a finite series or the nth partial sum of the sequence.}

_{Finding the Sum of a Series:}

_{Example 1:}

Example 2:

If all fails, you must enter the problem into a calculator.

In order to do this, you must follow this process:

2nd stat

math---> sum

ops--->seq

in other words:

sum(seq(explicit formula, variable, lower limit, upper limit))

Chapter 9- Sequences and Series

Sequence
- Name of the series/function

- An infinite sequence is a function whose domain is set of positive integers.

- The function values are the terms of the sequence

ex. finding the first three terms of the sequence

Finding the nth term of a sequence:
ex. 1 , 3 , 5 , 7 , . . . .

Solution:

• n: 1 2 3 4 . . . n
• terms: 1 3 5 7 . . .
• apparent pattern: Each term is 1 less than twice n, which applies that

A Recursive Sequence

where

Factorial


special case, zero factorial can be defined as 0!=1

Evaluating factorial expressions:

Solving Exponential and Logarithmic Equations

There are two basic strategies for solving exponential and logarithmic equations:

1. One-to-One Properties

• if and only if
• if and only if

2. Inverse Properties

• 
• 

Strategies for solving Exponential and Logarithmic Equations

1. Rewrite the given equation in a form to use the One-to-One properties
2. Rewrite an exponential equation in logarithmic form and apply the Inverse Property
   
3. Rewrite a logarithmic equation in exponential form and apply the Inverse Property
   

For Example:



(One-to-One property)






Now you have to check your answers to make sure they are not negative (due to domain restrictions). We find that 6 works, however 1 does not.

Another example that we need to know:




Let





now substitute

and

and