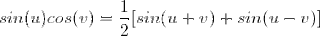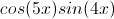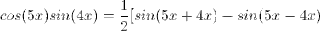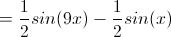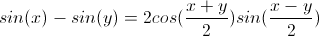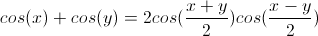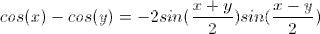Law of Sines

Trigonometry is about triangles

Triangels can be devided into two types

• Right -have a right angle (we like these)
  
• Oblique -do not have a right angle (Right triangles in training)

Unfortunalty, some important theorems only work with right triangles, these theorms include:

*Pathagorean theorm (insert formula picture)

*Sin, Cos, and Tan

Luckily, every Oblique triangle can be made into two right triangles!

• THE LAW OF SINES

  (a triangle with labed sides a, b, c and opposing angles, A, B, C)

  
  
  

  the LAW!
  

  
  

  The law of sines states that in every triangle, ratio of the sine of an angle over its opposite side is equal to every other sine of an angle over its opposite side in that triangle.

  While all of this is fine and dandy, it at first does not appear useful . . .

  But wait!

  this theorem allows one to find other angles or sides in Oblique triangles with only the information of:

• Two angles and a side
• Two sides and an angle
isn't that exciting?






(did I miss anything?)

Double-Angle Formulas

The most commonly used multiple-angle formulas are the double-angle formulas. They are used often and can be quite useful when we need to simplify complicated trigonometric expressions.

Sine of a double-angle

sin 2u = 2 sin u cos u

Cosine of a double-angle

Tangent of a double-angle

*Note that and

Suppose we wish to solve the equation cos 2x = sin x, for values of x in the interval −π ≤ x < π.

We would like to try to write this equation so that it involves just one trigonometric function, in

this case sin x. To do this we will use the double angle formula

cos 2x = 1 − 2 sin2x

The given equation becomes 1 − 2 sin2x = sin x which can be rewritten as 0 = 2 sin2x + sin x − 1

This is a quadratic equation in the variable sin x. It factorises as follows:

0 = (2 sin x − 1)(sin x + 1)

It follows that one or both of these brackets must be zero:

2 sin x − 1 = 0 or sin x + 1 = 0

so that sin x =1/2 or sin x = −1

Squaring and Converting to Quadratic Type

There maybe times when you run into an equation that needs to be squared on both sides to solve it. Here is how you go through that process, step by step:

Here's an example of a trigonometric equation:

To solve this equation, square both sides, which then changes it to this equation:

Now use one of the pythagorean identities to make all the variables cosines

Now the equation looks like this:

Combine like terms

Now factor

After setting each factor equal to zero and solving them, the answers are:

and

However, before we can say this is complete, since we squared the original equation we must check for extraneous solutions. After plugging all 3 possible answers into the original equation, we find that one does not work when plugged into the original equation.

Which leaves:

Power-Reducing Formulas/Half Angle Formulas

Power-Reducing Formulas

We can use the double angle formulas and derive them into the power-reducing formulas.

They are:

Most of the time, though, these formulas aren't useful because more often than not, we can use our other identities (such as the pythagorean identities) instead.

Half-Angle Formulas

From the power-reducing formulas, the half-angle formulas can be derived.

Product-to-Sum Formulas

Each of the following product-to-sum formulas is easily verified using the sum and difference formulas.

Example:

Sum-to-Product Formulas

Occasionally, it is useful to reverse the procedure and write a sum of trigonometric functions as a product. This can be accomplished with the following sum-to-product formulas. These formulas are useful for equations with different angles.

Monday April 11th, 2011

Today we learned more about chapter 5. We didn't learn any new identities unfortunately, but we did learn some rules to help make solving these problems a little easier.

The rules are....

1. Always work with one side of the equation and don't touch the other one.

2. Always look for ways to factor the expression first. If the expressions factor, its the first thing you should look for. Add fractions, square a binomial, or create a monomial denominator

3. Look for ways to use the identities. decide which functions are in the final expressions you want. Sines and cosines pair up nicely, as well as secants and cosecants and cotangents.

4. If the above rules haven't helped so far, try converting all terms to sines and cosines.

5. If all else fails, try something. Making an attempt is the first step in solving the problem!!

The homework was 5.1 numbers, 75, 78-80......5.2 numbers 19-22, 26-28, 40-43, 46, 51

Enjoy!!! :D