Thursday March 31, 2011

Today we jumped into the exciting new world of Chapter 5. Chapter 5 deals with Identities.

An identity function is defined as a function in which the domain values do not change at all. F(x)=x.

Today we learned a few of the many identities..

Reciprocal Identities

csc(x)= 1/sin(x) sec(x)=1/cos(x) cot(x)=1/tan(x) sin(x)=1/csc(x) tan(x)=1/cotan(x)

Quotient Identities

cotan(x)=cos(x)/sin(x)

Pythagorean Identities

sin²(x)+cos²(x)=1 tan²(x)+1=sec²(x) cotan(x)+1=csc²(x)

Even/Odd Identities

sin(-x)=-sine(x) csc(-x)=-csc(x) cos(-x)=cos(x) sec(-x)=sec(x) tan(-x)=-tan(x)

cotan(-x)=-cotan(x)

Co-Function Identities

sin(x)=cos(π/2-(x)) cos(x)=(pi/2-(x))

tan(x)=cotan(pi/2-(x))

sec(x)=csc(pi/2-(x))

csc(x)=sec(pi/2-(x))

cotan(x)=tan(pi/2-(x))

wow gold


soft



lv

Multiplicity

Today we learned about multiplicity regarding two different subjects.

1. Multiplicity of zeroes
2. Multiplicity of asymptotes

MULTIPLICITY OF ZEROES
Zeroes are found in the numerator of a rational function. 
If there is a factor with a multiplicity of one, then the line will cross the axis at that intercept.



For example:


If there are factors of a rational function that have an even multiplicity, it means that the line will be tangent (only touching it at one point) to the axis.
For example:


If there are factors that have an odd multiplicity, it means that the line lingers and levels off around the intercept, but does cross the axis at that point. 
For example:



MULTIPLICITY OF ASYMPTOTES
Asymptotes are found in the denominator of a rational function.
If an asymptote has an odd multiplicty, then the graph will behave oppositely on either side of the asymptote.
For example: 

It goes down on the left side of the asymptote and up on the right side.

If an asymptote has even multiplicity, then the graph will behave the same way on either side of the asymptote.


It goes up on both sides of the asymptote.

How to Graph Rational Functions

In order to graph a rational function you must determine four things:
1. x-intercepts
2. y-intercepts
3. vertical asymptote
4. horizontal asymptote

Lets start with something easy...

First, we find the x-intercepts:

(x-2) (x+3)=0

x=2      x= -3

Then, the y-intercepts:

y=  

y=1

When you find the vertical asymptote, you want to find where the fraction is undefined.

 

The denominator:

=0

(x+2) (x-3)=0

x= -2   x=3

Lastly, we find the horizontal asymptotes. Since both leading coefficients have the same degree, we take the ratio of the leading coefficients.

y=1

Shown in the graph above:

• the x-intercepts are at x= -3 and x=2
• the y-intercept is at y=1
• the asymptotes are labeled correctly and are shown with dotted lines

Graphing is a little more complicated...

If there is a hole in the graph.

For instance, lets take the equation:

Since the factor (x-3) is found in both the numerator and denominator, it can be canceled out, creating a whole in the graph.

Therefore, x=3 is not considered a y-intercept

To graph this:

• x-intercepts: x= -1  x=4
• y-intercept: y=2
• V.A.: x= -2   x=2
• H.A.: y=2
• hole in graph: x=3

The arrow is pointing to the hole in the graph where x=3. You singnify the hole with an open circle.

Lastly, to know whether the graph is going up or down, you look where the x-intercepts are. If there is no x-intercept where you are graphing it goes the opposite direction.

For example:
In the graph above, there is no x-intercept to the left of the vertical asymptote x= -2, so the graph would be going up.  The graph in the middle of the two asymptotes needs to touch the x- and y-intercept. The graph on thr right of the vertical asymptote x=2 is going down because it also needs to go through the x-intercept x=4.

Chapter 2.6: Rational Functions

Rational functions [R(x)] are any functions that can be written as

when both f(x) and g(x) are polynomials (Fraction = RATIO ; RATIOnal function, get it??)

Because R(x) is a fraction, there are some values for X and Y which make R(x) UNDEF

INED

These values are called ASYMPTOTES

On a graph, asymptotes appear as dotted lines where the graph does not cross

There are two types of asymptotes, Vertical (Y), and HORRIZONTAL (X)

any value that makes g(x) = ZERO is a VERTICAL ASYMPTOTE

Set g(x) = ZERO and solve for x (The solutions are -4 , 3)

When x is -4 or 3, g(x) = ZERO, and R(x) becomes UNDEFINED

X CANNOT be equal to -4 or 3

This creates VERTICAL asymptotes at X = -4 and X = 3

HORIZONTAL asymptotes are a little more tricky

3 rules:

1. Horizontal Asymptote (HA) is ZERO when the highest degree of the Numerator is SMALLER than the highest degree of the Denominator

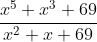
ex: (5 > 2)

2. If Highest degree of numerator is BIGGER than the highest degree of the denominator,

There is NO horizontal asymptote

ex: 100 > 4 so there is NO Horizontal asymptote

3. If highest degrees of numerator and denominator are EQUAL,

HA = Coefficient of highest degree term in Numerator

__________________________________

Coefficient of highest degree term in Denominator

ex:

4 / 2 = 2

HA = 2