Double-Angle Formulas

The most commonly used multiple-angle formulas are the double-angle formulas. They are used often and can be quite useful when we need to simplify complicated trigonometric expressions.

Sine of a double-angle

sin 2u = 2 sin u cos u

Cosine of a double-angle

Tangent of a double-angle

*Note that and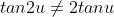

Suppose we wish to solve the equation cos 2x = sin x, for values of x in the interval −π ≤ x < π.

We would like to try to write this equation so that it involves just one trigonometric function, in

this case sin x. To do this we will use the double angle formula

cos 2x = 1 − 2 sin2x

The given equation becomes 1 − 2 sin2x = sin x which can be rewritten as 0 = 2 sin2x + sin x − 1

This is a quadratic equation in the variable sin x. It factorises as follows:

0 = (2 sin x − 1)(sin x + 1)

It follows that one or both of these brackets must be zero:

2 sin x − 1 = 0 or sin x + 1 = 0

so that sin x =1/2 or sin x = −1