Each of the following product-to-sum formulas is easily verified using the sum and difference formulas.
Example:
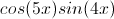
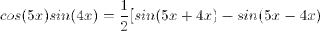
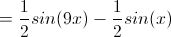
Sum-to-Product Formulas
Occasionally, it is useful to reverse the procedure and write a sum of trigonometric functions as a product. This can be accomplished with the following sum-to-product formulas. These formulas are useful for equations with different angles.
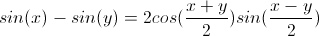
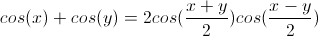
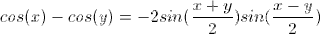
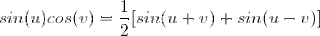
No comments:
Post a Comment