PreCalculus B 2nd Hour Spring 11: Chapter 9: Summation Notation

Sunday, May 22, 2011

Chapter 9: Summation Notation

Letter a is our first index, and letter b is our last index or upper limit. The variable(s) are the letters or the numbers that appear constantly in all terms.

Examples:

1.	$(a - 1) + (a^2 - 2) + (a^3 - 3) + (a^4 -4)$	$\displaystyle\sum_{i=1}^{4} (a^i - i)$
2.	$3p_5 + 3p_6 + 3p_7 + 3p_8$	$\displaystyle\sum_{j=5}^{8} 3p_j$
3.	$5 + 5 + 5 + 5 + 5 + 5 + 5$	$\displaystyle\sum_{k=1}^{7} 5$
4.	$1 + 2 + 3 + \cdots + 99 + 100$	$\displaystyle\sum_{m=1}^{100} m$
5.	$(a_3 + b_3) + (a_4 + b_4) +(a_5 + b_5)$	$\displaystyle\sum_{n=3}^{5} (a_n + b_n)$

Properties of Sums:

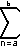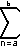$sum (k=a..b)$ c a_n = c $sum (k=a..b)$ a_n c is any constant

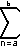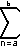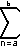$sum (k=a..b)$ a_n + $sum (k=a..b)$ b_n = $sum (k=a..b)$ (a_n + b_n)

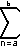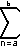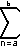$sum (k=a..b)$ a_n - $sum (k=a..b)$ b_n = $sum (k=a..b)$ (a_n - b_n)

Many applications involve the sum of the terms of an infinite sequence. Such a sum is called an infinite series or simply a series.

_{The sum of the first n terms of the sequence is called a finite series or the nth partial sum of the sequence.}

_{Finding the Sum of a Series:}

_{Example 1:}

Example 2:

If all fails, you must enter the problem into a calculator.

In order to do this, you must follow this process:

2nd stat

math---> sum

ops--->seq

in other words:

sum(seq(explicit formula, variable, lower limit, upper limit))

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)