-The Sum of Rows is equal to 2 to the power of that row.
| 20 = 1 21 = 1+1 = 2 22 = 1+2+1 = 4 23 = 1+3+3+1 = 8 24 = 1+4+6+4+1 = 16 -Another important pattern is the Hockey Stick Pattern: When adding up all of the numbers in a diagonal (leaving out the last number in the diagonal), the sum of those numbers will equal the last number of the diagonal. |
1+6+21+56 = 84
1+7+28+84+210+462+924 = 1716
1+12 = 13
nCr
1+7+28+84+210+462+924 = 1716
1+12 = 13
nCr
n= Row number (# of different items)
r= Diagonal (# of Combinations selected at a time)
1.)To find 6C4, you would go down the 6th row, and 4th diagonal and your answer would be 15.
6C4= 152.) Find 10C7.
Plug it into the calculator.
Expanding Binomials
Solve.


-If the binomial is a subtraction, the signs of the expanded form alternate between +/-





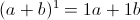

No comments:
Post a Comment