Chapter 12.2
Techniques for Evaluating Limits
Limits of polynomial and rational functions:
- if p is a polynomial function and c is a real number, then

- If r is a rational function given by r(x)=p(x)/q(x), and c is a real number such th
 at
at
then
Direct substitution
To find limits Algebraically (through direct substitution):
1) Factor the numerator and then
2) Cancel out the variables that can cancel
*limits can be found even if a hole does not allow the original problem to work out, but if there's a vertical asymptote, the limit does not exist (DNE)
example:
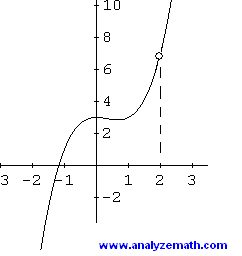
Continuous and discontinuous functions
For a graph to be continuous, it must fit this fornula:
the left and right side-limits must be equal to each other and must both be equal to the function
(the (+) sign as a superscript means the limit is right-sided and the (-) sign means the limit is left-sided)
Discontinuity is when a function os not continuous
Discontinuity can occur due to three things:
1) holes
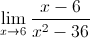
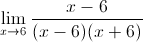





No comments:
Post a Comment