Reciprocal Identities:
Quotient Identities:
Pythagorean Identities:
Cofunction Identities:
And finally, Even/Odd Identities
Verifying/Solving Identities:
EXAMPLES:
Solving Trig Identities:
EXAMPLES:
Another Example:
Sum and Difference Formulas:
Once we have formulas for angle addition, angle subtraction is easy to derive. We just look at  and can derive the sine angle subtraction formula using the sine angle addition formula.
and can derive the sine angle subtraction formula using the sine angle addition formula.
Double Angle Formulas:
Half- Angle Formulas:
And finally, Sum to Product Formulas:
_______
This test will require lots of reviewing and studying. Practice all old homework and notes, and make sure to understand the Review Problems. If you do, you will most likely succeed on the final!
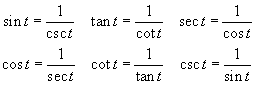
No comments:
Post a Comment